パップス・ギュルダンの定理－体積計算等に便利な定理－

パップス・ギュルダンの定理とは

パップス・ギュルダンの定理は、ある図形をある直線のまわりに回転させたときの体積は、回転体の図形が、できる立体に重ならなければ、回転体の図形の面積にその図形の重心が回転によって動く長さの掛け算として表されるというものです。これを使えば、回転体の体積は割合簡単に求まります。ただし、最近の入試問題では、パップス・ギュルダンで一発で求まるような問題は出さないように出題側も考慮しているようですが、覚えておくと便利なものと思います。中学入試や高校入試に使えるかもしれませんね。

簡単な応用例

半径ｒの半円の重心を求めるのに、パップス・ギュルダンの定理を逆に使ってみます。重心Ｇは、半円の中心Ｏとその直径に直交する直線上にありますから、これをＯからの距離をｘgとします。きゅうは、直径の直線ｌのまわりに回転したもので、体積Ｖ＝4/3・π・ｒ＾3です。そして、重心Ｇの動く距離は、２πｘg　となります。半円の面積Ｓ＝1/2・πｒ＾2ですから、パップス・ギュルダンから、

4/3・π・ｒ＾3＝２πｘg・Ｓとなりますから、ｘg＝4ｒ/3π　となります。

応用例２

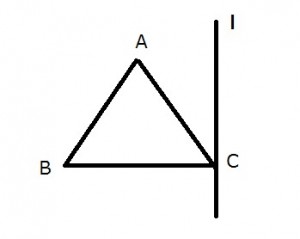
下の図のような直線ｌと正三角形ＡＢＣがあるとします。正三角形の一辺の長さはａとし、ＢＣ⊥直線ｌとします。この時、直線ｌの回りに三角形ＡＢＣを回転した時にできる立体の体積は、どうなるでしょうか。通常は回転体の体積から円錐を引けば出ますが、もちろん積分しても容易です。

パップス・ギュルダンなら、⊿ＡＢＣ＝√3/4・ａ^2で重心とｌの距離はａ/2ですから、ｌの回りにまわした曲線の長さ（円）は２･ａ/2・π＝aπです。従って、回転体の体積は、パップス・ギュルダンから、

√3/4･ａ^2・ａπ＝√3/4・πａ^3　となります。