ニュートン・ラフソン法－代数曲線のx軸との交点を求める方法－

ニュートン・ラフソン法とは

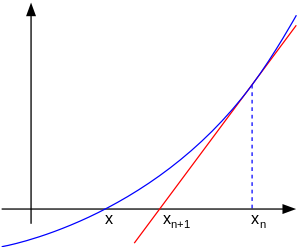
下図のように、ｘｙ平面上に、曲線f(x)があり、x軸と交点を持つとします。すなわち交点は、f(x)＝０との解を求める事と同値です。

この交点の値（近似値）を求める方法に、ニュートン・ラフソン法があります。

 

ニュートン・ラフソン法は、ｙ＝f(x)の交点の近傍に、あるｘ＝ｘnをとります。この時の曲線上の点Pの座標は、P(ｘn、f(ｘn))となります。

f(x)は、微分可能だとすると、Ｐにおける接線の傾きは、ｆ’(ｘn）となりますから、接線の方程式は、ｙ＝ｆ’(ｘn)（ｘ－ｘn）+ｆ(ｘn)　となります。これのx軸との交点を求めると、ｘ＝ｘn+1＝ｘn－ｆ(ｘn)/ｆ’(ｘｎ）となります。但し、ｆ’(ｘ）≠０だとします。これを、繰り返すと、数列

ｘn、ｘn+1、･････････を考える事ができます。ｎ→∞とすれば、この数列の極限値が、ｘ軸との交点の座標、すなわちｆ(x)=０の解となると言う訳です。

この方法を応用した、数列や極限の問題が結構あります。

類題

ａを正の定数とします。f(x)=ｘ^2－ａとし、ｙ＝ｆ(x)上の点（xn,ｆ(xn))における接線が、ｘ軸と交わる点のｘ座標をｘn+1とします。このようにして、ｘ1、ｘ2、････････を作る時に、次の問いに答えてください。ただし、ｘ1＞√ａとします。

（１）ｘｎ+1をｘｎで表してください。

（２）lim(n→∞)ｘnを求めてください。　（名古屋大　改）